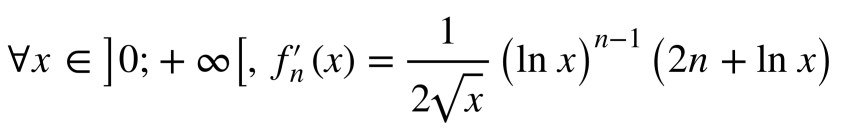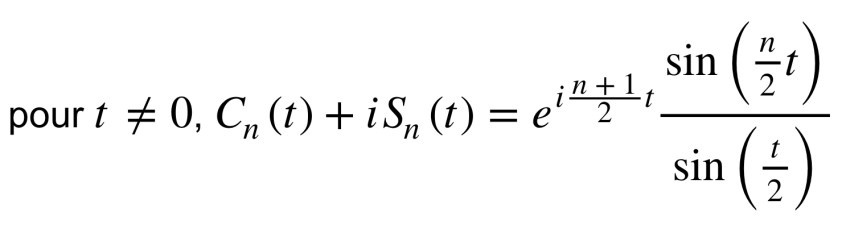suites

Bac S 2007 Métropole – corrigé complet

Pour ce post, je vous propose le sujet du bac S 2007 proposé en métropole. J’ai vu que The Maths Tailor en parlait sur sa chaîne : https://youtube.com/@TheMathsTailor?si=fFG-5wNQ0Odp3QjJ, encore une chaîne à fortement recommander ! Comme d’habitude, merci à l’APMEP de mettre tous ces sujets à disposition.

Vu les thèmes abordés dans ce sujet, je pense que c’est plus à aborder dans une perspective de prépa que pour le bac en lui-même, mais voyons ce qu’il en est.

Le 1er exercice nous fait étudier 2 plans et une droite. Pas sûr qu’on en croise encore souvent, même si les connaissances requises restent accessibles (la formule de la distance d’un point à un plan est une « extension » de la formule d’un point à une droite dans le plan par exemple). La dernière question est intéressante !

On continue avec une restitution de connaissance puis son application sur l’intégration par parties. À connaître par cœur bien sûr ! On retrouve dans l’application les fonctions exponentielles et trigonométriques si propices à l’intégration par parties, comme on l’a déjà vu ici (n’hésite pas à te pencher sur les intégrales de Wallis pour aller plus loin).

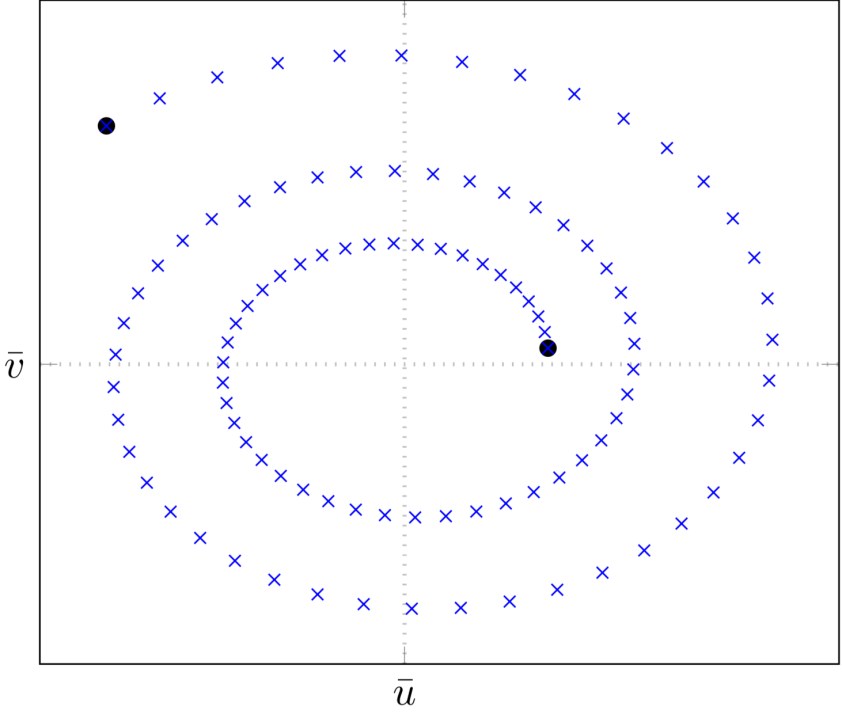
L’exercice 3 (spécialité ou non) nous emmène dans le monde merveilleux des complexes et des transformations du plan associées. Si tu es en maths expert, je te recommande de faire les 2 bien sûr. Celui de spécialité va un peu plus loin et te permet de t’assurer que tu maîtrises bien les concepts introduits avec du calcul évidemment et plusieurs transformations pour manipuler la norme, le conjugué ou la forme exponentielle.

Quelques questions en format QCM sur les probabilités pour l’exercice 4. Pour s’entraîner, le plus important est la justification.

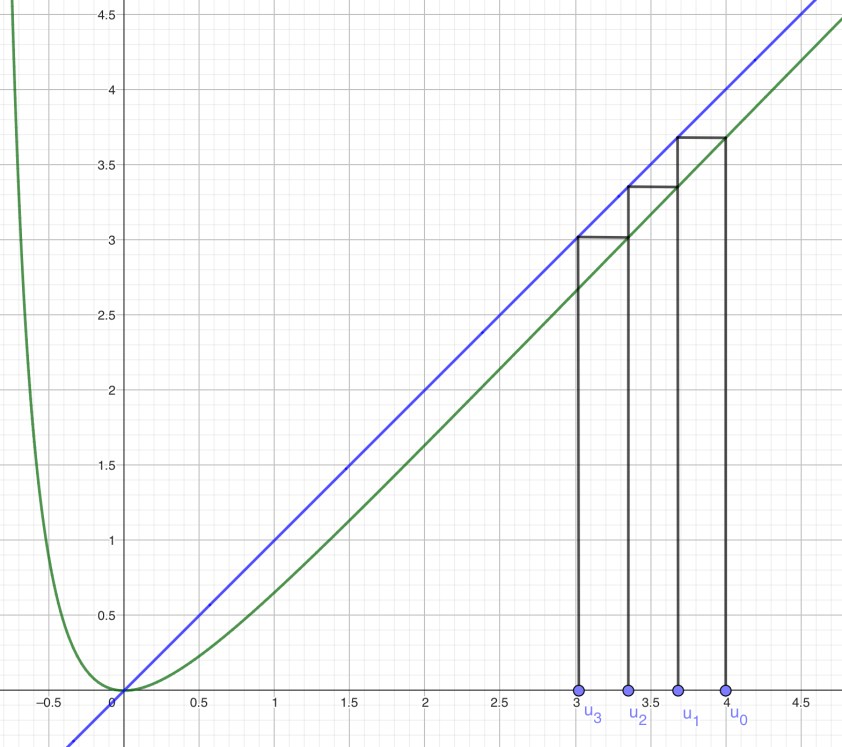
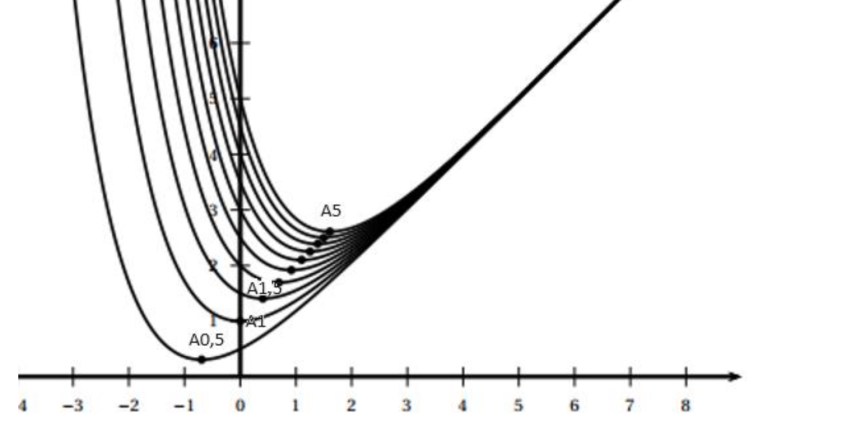
On finit sur une étude fonction à partir de laquelle on va définir une suite récurrente dont on va chercher la limite. On retrouve les éléments classiques de ce genre d’exercices avec un soupçon de logarithme. Dérivation, point fixe, monotonie d’une suite…

Au final, un sujet qui balaye large et constitue une bonne révision pour le bac et la suite !

Le sujet :

bac-s-2007-metropoleTélécharger

La correction :

bac-s-2007-metropole-corrigeTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

CAPES Mathématiques 2024 – Épreuve 1

Je pense que c’est assez connu, le CAPES est le concours de recrutement des enseignants du second degré, collège et lycée. L’écrit de ce concours est composé de 2 épreuves, une constituée de problèmes dans la discipline concernée et une dans laquelle on évalue des réponses potentielles d’élèves, évidemment toujours dans la discipline. Bref ! Aujourd’hui je vous propose de balayer la première épreuve.

J’ai déjà dit que je n’aimais pas les VRAI/FAUX, où on enchaîne les questions sans rapport les unes avec les autres et où (parfois) tout le sel réside dans une formulation subtilement trompeuse… Bon, après il ne faut pas non plus se chercher des excuses, mais ça ne permet pas des problèmes passionnants. Eh bien me voilà servi avec 23 questions et à peu près la moitié du sujet ! On parcourt une large part des thèmes du lycée avec proportionnalité, analyse (surtout sur les intégrales), arithmétique (et un peu de logique), géométrie (dans l’espace), probabilité et algorithmique. Il faut bien connaître le cours (vous me direz que c’est bien le minimum si on veut être professeur !), mais pas grand chose de palpitant. Qui a dit au fond de la salle que je pouvais réviser la loi de Poisson ?? Oui, bon, ça va hein, ça arrive à tout le monde un moment de faiblesse ! D’ailleurs, à choisir la partie probabilité m’a plutôt plu avec des questions un peu différentes des habitudes.

Passons au problème d’analyse qui va nous faire étudier des modèles d’évolution de populations. Étude de fonction, suites, un peu d’équations différentielles et d’algèbre linéaire à la fin. Le principe est plutôt intéressant et on compare le comportement asymptotique de ces différents modèles.

Au final, pas de grosse difficulté dans le sujet mais une bonne occasion de réviser avant le bac ! Ou même en L1, je pense que ça ne fait pas de mal.

Le sujet :

capes-2024-epreuve-1Télécharger

Le corrigé :

CAPES 2024 – Epreuve 1 – corrigéTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Bac Maroc 2023 – Rattrapage – corrigé complet

Les sujets des épreuves de maths du bac au Maroc sont l’objet de pas mal de discussions tous les ans. Je n’avais pas vu passer jusqu’ici d’épreuve de rattrapage… Je me suis donc penché dessus et le moins qu’on puisse dire est que je n’ai pas été déçu ! Tuons le suspens, je pense qu’il valait mieux réussir la première épreuve, ce rattrapage étant au moins aussi difficile, voir même plus.

Regardons un peu tout ça ! On reste dans l’esprit des sujets que j’ai partagé précédemment et on attaque sur un long exercice d’analyse, découpé en 3 parties : on étudie d’abord les propriétés générales d’une famille de fonctions définies avec un paramètre n. On continue avec une suite définie par une valeur particulière de chaque fonction f_n . Questions classiques de monotonies et limites… On finit par du calcul d’intégrale. Une étude très complète donc et vraiment pas facile !

Les 3 exercices suivants sont plus courts. On enchaîne avec un exercice sur les complexes qu’on introduit via un système de 2 équations à 2 inconnues qui vont être liées aux parties réelles et imaginaires d’un complexe z. La 2ème partie n’est pas liée et propose une approche via les complexes d’un problème de géométrie. Dans cette partie, on peut insister une fois de plus sur la puissance des nombres complexes comme « extension » de la géométrie cartésienne.

La suite est « traditionnellement » sur les structures algébriques, mais cette fois, on ne reste pas sur les habituelles (et encore, seulement en maths expertes chez nous) manipulations de matrices, mais on introduit des structures et des opérations assez inédites. Même si ces dernières restent à base d’arithmétique, leur manipulation demande une bonne maîtrise des concepts sous-jacents car on peut vite se perdre sinon !

Pour les survivants, on finit avec un peu d’arithmétique et de congruence. Là encore un exercice assez court, mais pas facile pour autant. On se rappelle si besoin, que sous leur air gentillet, ces exercices peuvent vite demander de se creuser la tête pour trouver les bonnes idées !

En conclusion, encore un très bon cru venu du Maroc, même si je ne sais pas si beaucoup ont eu l’occasion de se rattraper avec cette épreuve ! J’avais récupéré ce sujet il y a un moment, donc je ne sais plus trop où, mais merci à celle ou celui qui avait partagé ! Allons-y !

bac-sm-rattrapage-2023Télécharger
bac-maroc-maths-sept-2023-corrigeTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Bac C 1981 – Aix Marseille – corrigé complet

Repartons à la rencontre des sujets qui ont fait pleurer les élèves en leur temps avec ce sujet de 81 pour l’académie d’Aix Marseille. J’avais entendu parler de ce sujet il y a quelques temps et il m’est revenu en tête à la publication de la vidéo d’Axel Arno (https://youtu.be/XYKocUhk4Ng?si=cN9XNH4Un6opnOns. Je n’ai pas encore regardé la vidéo au moment où j’écris cet article, mais je ne doute pas qu’elle vaille le coup !). Je n’ai pas été déçu du voyage !

On s’échauffe tranquillement avec un raisonnement par l’absurde sur les nombres premiers. On est dans du classique, mais cet exemple est à maîtriser.

L’exercice 2 est de la géométrie. Sans être forcément difficile, il est assez bourrin avec une composition de 4 transformations. Pas mal de calculs, j’espère ne pas avoir fait d’erreur, j’avoue avoir eu la flemme de relire !

On arrive sur le gros morceau, le problème de Bâle ou le calcul de la somme des inverses des carrés. On va donc manipuler des suites dans un premier temps (ça reste le thème de base) pour s’assurer d’abord de la convergence de la somme. On continue ensuite avec de la trigonométrie, en faisant un détour par les complexes tant qu’à faire. Je pense que cette partie n’est plus vraiment accessible en terminale, les complexes n’étant abordés qu’en maths expertes. On s’étonnera au passage qu’un résultat assez basique (la somme des termes d’une suite géométrique) soit rappelé dans l’énoncé quand on voit les connaissances nécessaires pour traiter le problème.

Avant de conclure, on passe par des études de fonctions et des calculs d’intégrales dont on va chercher les limites… L’arrivée à ce magnifique résultat sera la consécration de tous ces efforts !

En selle, voici le sujet :

bac-c-1981-aix-marseilleTélécharger

Et la correction :

Bac C 1981 – Aix Marseille – corrigéTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Bac 2024 – sujet 0 – corrigé complet

Je finis donc dans ce post le corrigé du sujet 0 du bac 2024. Comme ça, le sujet est dans le premier post et la correction complète est là. Si avec ça je ne génère pas un trafic de malade dans le coin, c’est à n’y rien comprendre !

Bref, je m’étais arrêté la dernière fois car la première partie du sujet est assez dense déjà et qu’en plus on enchaîne sur 2 exercices de QCM sans justification, ce qui reste pour moi totalement incompréhensible et à l’opposé de l’esprit que devrait avoir un sujet de math. J’en ai déjà parlé, je n’insiste pas (mais ça m’agace toujours autant…). J’ai quand même pris la peine de justifier les réponses, histoire de garder un semblant d’intérêt quand même.

On attaque donc sur un exercice de géométrie dans l’espace. Tout est dommage dans cet exercice, vu le format, on survole uniquement les thèmes abordés, forcément. On revoit quelques points sur les vecteurs.

L’exercice suivant est sur le même principe mais en plus les 5 questions sont sur 2 thèmes sans rapport entre eux. On part sur 2 questions sur la fonction sinus… pour partir ensuite sur du dénombrement. Admettons… Il faut un peu d’attention pour la fonction sinus, mais rien de palpitant. Concernant le dénombrement, je pense avoir déjà précisé ne pas aimer ces chapitres, mais (du coup ?) je trouve que c’est toujours important de réviser.

Un peu de suites et de récurrence pour les exercices 6 et 8, dommage de ne pas aller plus en profondeur, les questions sont assez similaires dans les 2. Un peu comme le QCM, je trouve que le format « vrai/faux » n’est pas vraiment propice à une étude un peu approfondie. EDIT : on m’a remonté une erreur dans l’exercice 8, ça m’apprendra ! Comme quoi, il faut toujours rester attentif…

Le dernier exercice (enfin l’avant-dernier dans l’ordre) est sur le même principe de vrai/faux mais a propos de l’étude d’une famille de fonctions. Ça aurait pu être intéressant (par exemple les minimas alignés), mais là encore le format gâche le plaisir.

Bref, voyons quand même le positif de ce sujet : les 3 premiers exercices étaient intéressants et la suite reste un prétexte pour réviser en attendant le véritable sujet !

Bac 2024 – sujet 0 – completTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Bac S 1996 – Asie – corrigé complet

Pour ce dernier post de l’année, je vous propose un dernier sujet de bac que j’ai trouvé plutôt varié et donc intéressant.

On commence avec un exercice de probabilités assez standard. Il reste d’actualité, car on y revoit les formules principales qu’on trouve dans tous les sujets actuels ! (Enfin, c’est l’impression que ça m’a donné ces dernières années). On tire une boule, puis 3 et on passe par les probabilités totales puis conditionnelles.

Comme souvent autour de cette période, l’exercice spécifique à l’enseignement obligatoire s’intéresse aux complexes (ça fait toujours un peu mal de penser que c’est réservé en maths expert maintenant, quand on pense simplement au voyage intellectuel depuis leur « création » jusqu’à leur importance en physique actuellement !). On y étudie une transformation sous un angle analytique puis géométrique. Cela permet de revoir une bonne partie des propriétés du programme, l’utilisation de l’expression conjuguée, les propriétés d’un quotient de 2 complexes…

Pour l’exercice 2 de spécialité, on étudie une fonction paramétrique, là encore en 2 temps : tout d’abord une étude directe puis une étude via une transformation dans le plan complexe. Pour la première partie, je ne sais pas si ça se pratique encore beaucoup aujourd’hui ! En tout cas, je n’en ai pas vu depuis un moment, à part pour des choses très basiques comme des droites ou des plans dans l’espace. Bref, cela oblige à revenir aux bases de certains concepts, comme la dérivée par exemple, on ne peut pas utiliser les formules classiques sous cette forme. La 2ème partie avec la transformation complexe est assez amusante, car finalement on « devine » plus facilement la forme de la courbe ! (Enfin, il faut d’abord connaître le résultat pour pouvoir le proposer cela dit…)

On finit sur un problème d’analyse. On est sur une fonction très standard, qu’on peut trouver encore aujourd’hui d’ailleurs, à base de logarithme. Pas grand chose à ajouter, on va cependant balayer une bonne partie des concepts du secondaire : étude de fonction, intégrales et utilisation de suites pour approcher une valeur particulière.

Au final, un beau sujet pour finir l’année ! J’en profite pour remercier tous ceux qui ont venus sur ce blog pendant l’année, j’espère que ça aura pu vous être utile ou, au moins, que ça aura piqué votre curiosité !

Sujet :

bac-s-1996-asieTélécharger

Corrigé :

bac-s-1996-asie-1Télécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Dérivation exos 158 à 161

Repartons dans le poly LLG avec 4 exercices sur les dérivées.

On a 3 exercices qui nous font manipuler les propriétés des dérivées et des tangentes aux courbes. Rien de bien particulier à signaler, mais c’est à bien maîtriser.

J’ai surtout voulu partager le 161, qui va nous faire étudier la technique de Newton pour calculer les racines carrées. On étudie d’abord une fonction qui sert à définir la suite des valeurs successives pour approcher la racine à calculer et finalement s’intéresser à la vitesse de convergence. Encore un bel exercice qui nous permet d’utiliser plusieurs techniques du programme, c’est souvent ce qui donne les exercices les plus intéressants bien sûr.

Je ne perds pas plus de temps avant de vous laisser retrouver Newton !

derivation-exos-158-a-161Télécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

On franchit la limite…

Un petit post pour finir le chapitre 5 du poly LLG sur les limites. Il s’agit des exercices 141, 142 et 143. Techniquement, le chapitre en propose un dernier, mais qui est extrêmement difficile et que je n’ai pas réussi à rédiger de façon satisfaisante.

Pour mémoire, comme ça fait un petit moment qu’on n’en a pas parlé, ces exercices sont issus du poly de transition de la terminale aux CPGE proposés par des professeurs de Louis-le-Grand. Il contient bien d’autres informations que les exercices que je partage sur ce blog. Je recommande à tout élève de Terminale, voir déjà en sup, de récupérer ce document.

Bref, concentrons nous donc sur les exercices en question.

On commence par des suites trigonométriques, dont le comportement n’est pas forcément simple à l’infini. Et d’ailleurs on conclut que les seules suites convergentes sont les suites triviales.

On attaque ensuite un exercice plus compliqué à bien mettre en équation. On s’intéresse au comportement des puissances de 2. Une fois que c’est fait, la résolution n’est plus très difficile.

On finit sur l’étude d’une suite définie par une somme de factoriels. Des indices de difficulté de 4, 4 et 5 plutôt mérités je pense.

À vous de jouer !

du-lycee-aux-cpge-calcul-de-limites-3-exosTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Bac série 2011 – Métropole

Bac 2011 aujourd’hui. Pourquoi ? Aucune raison, j’ai cliqué dessus dans la série des années et pas de regret, j’ai trouvé ce sujet bien intéressant. Comme quoi, il n’y a pas si longtemps on avait encore des vrais sujets au bac ! Plongeons-nous dedans !

On commence par des probabilités et… le calcul de la fiabilité d’un test de dépistage ! Situation presque encore d’actualité (voir qui a tendance à le redevenir…). En tout cas, on y revoit les grands résultats du programme et comme souvent avec les probabilités, on y croise des résultats plutôt contre-intuitifs.

Exercice 2, un QCM, toujours sans justification. C’est bien dommage, on y parle des complexes et les justifications y sont aussi importantes que les résultats en eux-même. Comme d’habitude, en exercice d’entrainement il faut absolument justifier les résultats.

Exercice 3 : un long exercice d’analyse, avec (comme assez souvent), un premier fonction dont l’étude nous sert, en partie, dans la suite. Le sujet concerne globalement une famille de fonctions, leurs courbes et des tangentes. Partie B, on étudie la suite des intégrale correspondantes. Classique mais intéressant et varié.

Exercice 4 – hors spécialité : j’ai été assez surpris par celui-ci car c’est un exercice de géométrie dans l’espace pas trivial du tout et assez long ! Je pense que ça a dû piquer sur pas mal de copies ! Il fallait bien connaitre les grandes propriétés des distances d’un point à un plan, des droites/vecteurs orthogonaux au plan…

Et du coup, l’exercice de spécialité parait un peu fade après ça (même s’il n’y a évidemment pas eu de « après » pour les bacheliers qui n’avait qu’un des 2 à traiter). On a droit à de l’arithmétique, c’est vrai qu’on n’en voit pas si souvent, mais bon… Bref… Les résultats importants sont rappelés, donc c’est juste pour voir si les élèves ont compris les congruences en gros. Dommage !

On ne boude pas son plaisir pour autant, un sujet qui balaye large et des exercices intéressants ! A vous de jouer !

bac-s-2011-metropoleTélécharger
bac-s-2011-metropole-1Télécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Bac série C 1992 – Métropole gr 1

Nouvelle annale de bac pour ce post, avec cette fois l’épreuve passée par mon grand frère. J’avoue que je n’ai pas des caisses de commentaires à faire sur l’épreuve en elle-même, je vais juste noter la remarque faite par l’APMEP : « le sujet sans difficulté majeure, où pratique- ment tous les résultats étaient donnés, a permis dans l’académie d’Amiens d’obtenir des moyennes nettement supérieures à 10. » Bah merci ! (Enfin, évidemment, merci une nouvelle fois pour le partage des ressources !)

L’épreuve est en 2 parties : les 2 exercices principalement sur de la géométrie et le problème sur de l’analyse.

Le 1er exercice est introduit par une équation du 3ème degré à résoudre dans C. Rien de particulier, on a une solution évidente comme première étape de résolution, puis un trinôme. C’est en fait une introduction pour placer des points et étudier une ellipse dans la question 2. Je crois que ça ne se fait plus trop, à part un peu dans sa version analytique et c’est dommage quand on voit l’importance de ces figures !

2ème exercice, à nouveau de la géométrie, sur des symétries et des triangles. Exercice assez basique, à part peut-être la propriété des points cocycliques, même si je pense que la propriété utilisée est toujours vue au collège cela dit…

On arrive sur le gros morceau, le problème d’analyse : étude de fonction paramétrique, suites, limites, intégrales… Je trouve que c’est un bon exercice de révision. En tant qu’épreuve, en effet, on revient sur la remarque de l’introduction, c’est très guidé et l’élève à l’aise se sent presque bridé par l’énoncé qui donne vraiment beaucoup d’indications. Je pense au passage qu’il serait intéressant de faire faire l’exercice par des terminales actuelles pour voir le résultat.

En tout cas, nous voilà partis !

bac-c-1992-metropole-gr-1Télécharger
bac-1992-serie-c-metropoleTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine