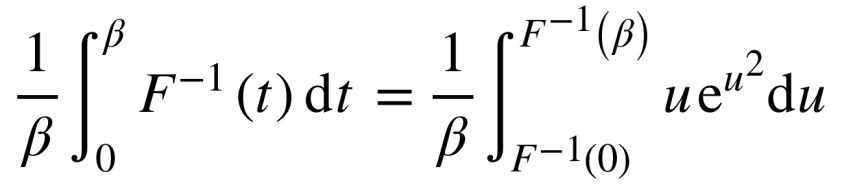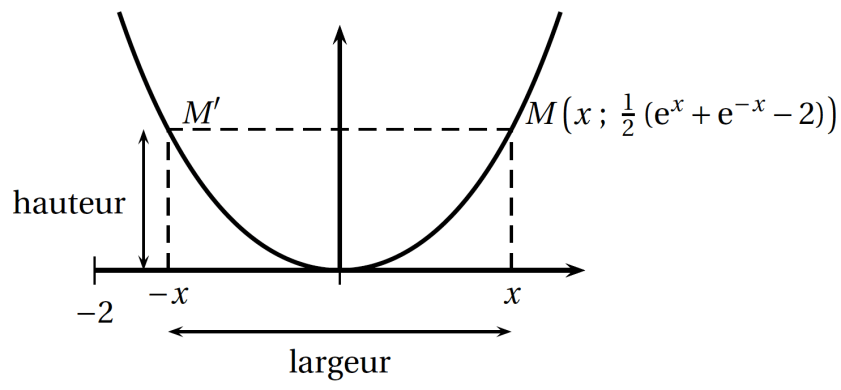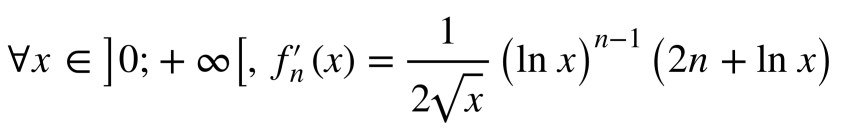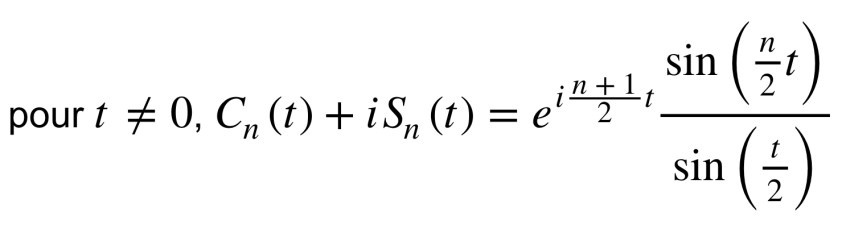Complexes

Bac SM 2024 – Maroc – corrigé complet

Le petit plaisir de l’année est donc sorti il y a quelques jours ! C’est désormais une forme de tradition, le sujet du bac marocain fait pas mal parler en France. Probablement à raison, mais là n’est pas l’affaire, c’est encore du lourd cette année ! Ne tardons pas plus.

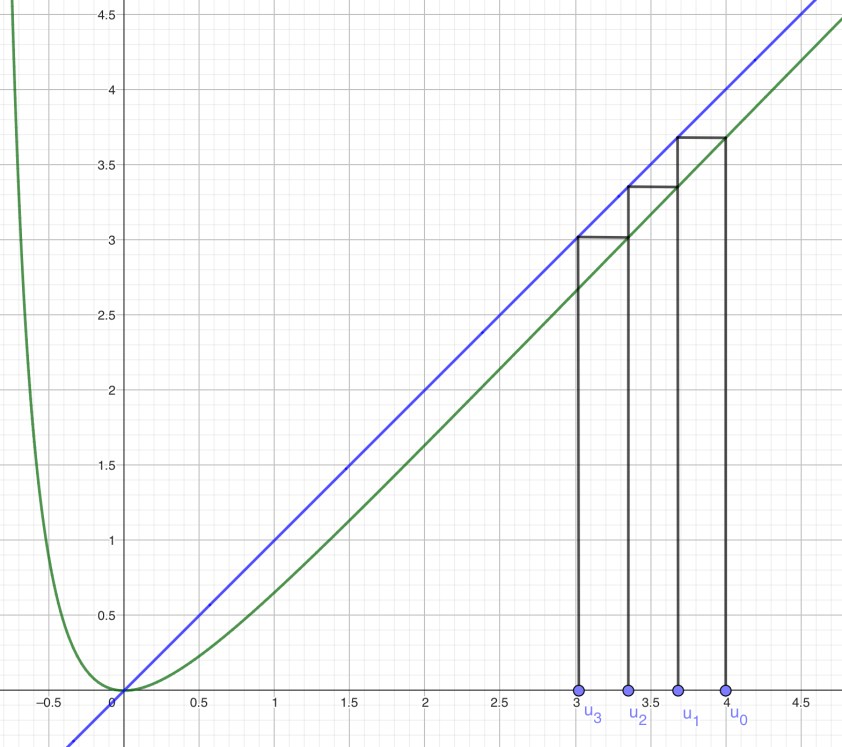
Comme ces dernières années, on attaque avec un gros exercice d’analyse. On étudie une fonction plutôt simple en apparence mais qui nous réserve bien des surprises, et plutôt des mauvaises bien sûr ! Changement de variable pour calculer des limites, limite de taux d’accroissement. On remarquera que même quand l’énoncé donne une indication, son utilisation n’est pas triviale. On passe par du calcul intégral pour étudier le sens de variation (surprenant !) puis une étude de point fixe avant de finir sur une suite « déduite » de la fonction. 7,5 points pour le tout, il faut les mériter.

La suite est moins aride, mais pas facile pour autant. On continue avec une fonction définie par une intégrale : théorème fondamental de l’analyse et changement de variable au programme pour calculer la limite d’une série.

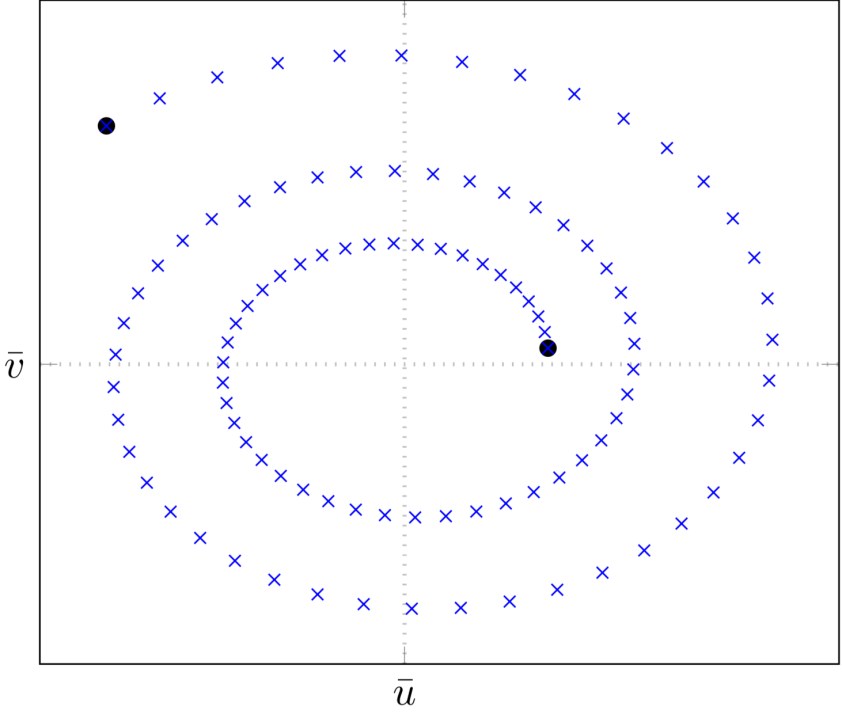
Ça continue avec un exercice sur les complexes : on étudie une équation du second degré avec coefficients complexes. Cela nous entraine avec les propriétés géométriques des points dont les affixes sont les solutions de l’équation. Je ne vais pas revenir sur ma marotte, mais ça manque vraiment dans le programme chez nous !

L’enchaînement est semblable aux précédentes éditions avec un peu d’algèbre. Exercice un peu basique par rapport à ce qu’on a déjà vu : on étudie de façon guidée les propriétés d’un groupe.

On finit avec de l’arithmétique sous l’ombre de Gauss et Fermat…

Un nouveau très beau sujet au final varié et difficile, pour passer un bon moment pendant l’été !

Le sujet :

Bac 2024 – MarocTélécharger

Le corrigé :

Bac 2024 – Maroc – corrigéTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelle aventures mathématiques !

Antoine

Bac S Liban 2018 – corrigé complet

Le bac de 204 commençant à se rapprocher dangeureusement, je vous propose un nouveau sujet à parcourir : Liban 2018.

On attaque tranquillement avec des variables aléatoires avec une loi exponentielle et une loi normale. On applique juste les formules du cours et on se rend compte que le standard d’appel n’est pas évident à joindre !

Exercice rapide pour les complexes pour les maths experts. On manipule les formes exponentielles et la formule de Moivre, ça ne fait pas de mal.

On enchaîne avec des sous-marins dans le déplacement est donné par des formules dépendantes du temps (linéaires). Aucune difficulté, il faut juste bien manipuler les petits systèmes des 3 coordonnées. Attention tout de même au calcul d’angle…

Une étude de fonction nous attend pour la suite. Une fonction classique avec des propriétés intéressantes, mais l’exercice laisse sur sa fin (on étudie sur un petit intervalle plutôt que sur tout l’ensemble de définition, un peu dommage, ça permettait d’ajouter une peu de limite par exemple). Il y a d’ailleurs un problème sur cette même fonction dans une autre épreuve ! Reste à retrouver où par contre…

On repart dans les probabilités pour l’exercice hors spécialité. Pas de piège particulier, mais un enchaînement sympathique proba qui glisse vers une étude suite.

On finit avec l’exercice spécialité avec des propriétés de la suite de Fibonacci amenées par une vision matricielle de cette suite. Original ! Merci à l’auteur.

Au final, une belle série d’exercices dans cette épreuve, même si on aurait bien voulu qu’au moins l’un d’entre eux soit développé en problème. À vous de jouer !

Le sujet :

bac-s-2018-libanTélécharger

Le corrigé :

bac-s-2018-liban-corrigeTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques.

Antoine

BAC S 2018 – Métropole – corrigé complet

Les révisions du bac vont bon train, je vous propose donc aujourd’hui d’étudier le sujet de 2018 en métropole (et la Réunion d’ailleurs). Je l’ai fait après être tombé sur un bel article du site Images des Mathématiques (hautement recommendable soit dit en passant) : https://images.math.cnrs.fr/Nombres-puissants-au-bac-S.html. Mauvaise pioche, l’exercice évoqué est le dernier du sujet !

On attaque sur un exercice d’analyse dans lequel on étudie une fonction exponentielle. On va chercher des points possédant une propriété particulière en introduisant une autre fonction qu’on va étudier en détails. On glisse un peu d’algorithmique pour finalement arriver sur un cas pratique.

On enchaîne sur un exercice de probabilités évoquant la diffusion d’une maladie, en fonction de la vaccination ou non des individus. Vu l’année, c’était la grippe évidemment ! Pas grand chose à dire, les questions sont très classiques, à maîtriser bien sûr !

L’exercice 3 propose de la géométrie dans l’espace et des propriétés des tétraèdres. On revoit une bonne partie des notions du programme, c’est intéressant. Toujours dommage qu’on n’en voit pas plus.

On bifurque ensuite pour l’exercice hors spécialité, qui nous propose une suite de nombres complexes dont on va étudier le comportement, puis des propriétés des points du plan dont les affixes sont les éléments de la suite. Evidemment, le public cible est plus restreint aujourd’hui, mais ça reste intéressant pour ceux qui sont en maths experts.

Et on finit donc par l’exercice sur les nombres puissants évoqué en introduction ! Exercice d’arithmétique avec un peu de matrice au milieu. Là encore on est sur le programme math expert mais c’est un exercice bien foutu et un bon enchaînement. Enfin, je ne pourrais pas en dire plus que l’article partagé !

Au final, un sujet très intéressant, même s’il ne s’adresse qu’à une frange réduite des élèves aujourd’hui… Enfin, je recommande tout de même pour ceux qui font maths experts ! Allons-y !

Sujet :

bac-s-2018-metropoleTélécharger

Corrigé :

bac-s-2018-metropole-corrigeTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Bac S 2007 Métropole – corrigé complet

Pour ce post, je vous propose le sujet du bac S 2007 proposé en métropole. J’ai vu que The Maths Tailor en parlait sur sa chaîne : https://youtube.com/@TheMathsTailor?si=fFG-5wNQ0Odp3QjJ, encore une chaîne à fortement recommander ! Comme d’habitude, merci à l’APMEP de mettre tous ces sujets à disposition.

Vu les thèmes abordés dans ce sujet, je pense que c’est plus à aborder dans une perspective de prépa que pour le bac en lui-même, mais voyons ce qu’il en est.

Le 1er exercice nous fait étudier 2 plans et une droite. Pas sûr qu’on en croise encore souvent, même si les connaissances requises restent accessibles (la formule de la distance d’un point à un plan est une « extension » de la formule d’un point à une droite dans le plan par exemple). La dernière question est intéressante !

On continue avec une restitution de connaissance puis son application sur l’intégration par parties. À connaître par cœur bien sûr ! On retrouve dans l’application les fonctions exponentielles et trigonométriques si propices à l’intégration par parties, comme on l’a déjà vu ici (n’hésite pas à te pencher sur les intégrales de Wallis pour aller plus loin).

L’exercice 3 (spécialité ou non) nous emmène dans le monde merveilleux des complexes et des transformations du plan associées. Si tu es en maths expert, je te recommande de faire les 2 bien sûr. Celui de spécialité va un peu plus loin et te permet de t’assurer que tu maîtrises bien les concepts introduits avec du calcul évidemment et plusieurs transformations pour manipuler la norme, le conjugué ou la forme exponentielle.

Quelques questions en format QCM sur les probabilités pour l’exercice 4. Pour s’entraîner, le plus important est la justification.

On finit sur une étude fonction à partir de laquelle on va définir une suite récurrente dont on va chercher la limite. On retrouve les éléments classiques de ce genre d’exercices avec un soupçon de logarithme. Dérivation, point fixe, monotonie d’une suite…

Au final, un sujet qui balaye large et constitue une bonne révision pour le bac et la suite !

Le sujet :

bac-s-2007-metropoleTélécharger

La correction :

bac-s-2007-metropole-corrigeTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

CAPES Mathématiques 2024 – Épreuve 1

Je pense que c’est assez connu, le CAPES est le concours de recrutement des enseignants du second degré, collège et lycée. L’écrit de ce concours est composé de 2 épreuves, une constituée de problèmes dans la discipline concernée et une dans laquelle on évalue des réponses potentielles d’élèves, évidemment toujours dans la discipline. Bref ! Aujourd’hui je vous propose de balayer la première épreuve.

J’ai déjà dit que je n’aimais pas les VRAI/FAUX, où on enchaîne les questions sans rapport les unes avec les autres et où (parfois) tout le sel réside dans une formulation subtilement trompeuse… Bon, après il ne faut pas non plus se chercher des excuses, mais ça ne permet pas des problèmes passionnants. Eh bien me voilà servi avec 23 questions et à peu près la moitié du sujet ! On parcourt une large part des thèmes du lycée avec proportionnalité, analyse (surtout sur les intégrales), arithmétique (et un peu de logique), géométrie (dans l’espace), probabilité et algorithmique. Il faut bien connaître le cours (vous me direz que c’est bien le minimum si on veut être professeur !), mais pas grand chose de palpitant. Qui a dit au fond de la salle que je pouvais réviser la loi de Poisson ?? Oui, bon, ça va hein, ça arrive à tout le monde un moment de faiblesse ! D’ailleurs, à choisir la partie probabilité m’a plutôt plu avec des questions un peu différentes des habitudes.

Passons au problème d’analyse qui va nous faire étudier des modèles d’évolution de populations. Étude de fonction, suites, un peu d’équations différentielles et d’algèbre linéaire à la fin. Le principe est plutôt intéressant et on compare le comportement asymptotique de ces différents modèles.

Au final, pas de grosse difficulté dans le sujet mais une bonne occasion de réviser avant le bac ! Ou même en L1, je pense que ça ne fait pas de mal.

Le sujet :

capes-2024-epreuve-1Télécharger

Le corrigé :

CAPES 2024 – Epreuve 1 – corrigéTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Bac Maroc 2023 – Rattrapage – corrigé complet

Les sujets des épreuves de maths du bac au Maroc sont l’objet de pas mal de discussions tous les ans. Je n’avais pas vu passer jusqu’ici d’épreuve de rattrapage… Je me suis donc penché dessus et le moins qu’on puisse dire est que je n’ai pas été déçu ! Tuons le suspens, je pense qu’il valait mieux réussir la première épreuve, ce rattrapage étant au moins aussi difficile, voir même plus.

Regardons un peu tout ça ! On reste dans l’esprit des sujets que j’ai partagé précédemment et on attaque sur un long exercice d’analyse, découpé en 3 parties : on étudie d’abord les propriétés générales d’une famille de fonctions définies avec un paramètre n. On continue avec une suite définie par une valeur particulière de chaque fonction f_n . Questions classiques de monotonies et limites… On finit par du calcul d’intégrale. Une étude très complète donc et vraiment pas facile !

Les 3 exercices suivants sont plus courts. On enchaîne avec un exercice sur les complexes qu’on introduit via un système de 2 équations à 2 inconnues qui vont être liées aux parties réelles et imaginaires d’un complexe z. La 2ème partie n’est pas liée et propose une approche via les complexes d’un problème de géométrie. Dans cette partie, on peut insister une fois de plus sur la puissance des nombres complexes comme « extension » de la géométrie cartésienne.

La suite est « traditionnellement » sur les structures algébriques, mais cette fois, on ne reste pas sur les habituelles (et encore, seulement en maths expertes chez nous) manipulations de matrices, mais on introduit des structures et des opérations assez inédites. Même si ces dernières restent à base d’arithmétique, leur manipulation demande une bonne maîtrise des concepts sous-jacents car on peut vite se perdre sinon !

Pour les survivants, on finit avec un peu d’arithmétique et de congruence. Là encore un exercice assez court, mais pas facile pour autant. On se rappelle si besoin, que sous leur air gentillet, ces exercices peuvent vite demander de se creuser la tête pour trouver les bonnes idées !

En conclusion, encore un très bon cru venu du Maroc, même si je ne sais pas si beaucoup ont eu l’occasion de se rattraper avec cette épreuve ! J’avais récupéré ce sujet il y a un moment, donc je ne sais plus trop où, mais merci à celle ou celui qui avait partagé ! Allons-y !

bac-sm-rattrapage-2023Télécharger
bac-maroc-maths-sept-2023-corrigeTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Bac C 1981 – Aix Marseille – corrigé complet

Repartons à la rencontre des sujets qui ont fait pleurer les élèves en leur temps avec ce sujet de 81 pour l’académie d’Aix Marseille. J’avais entendu parler de ce sujet il y a quelques temps et il m’est revenu en tête à la publication de la vidéo d’Axel Arno (https://youtu.be/XYKocUhk4Ng?si=cN9XNH4Un6opnOns. Je n’ai pas encore regardé la vidéo au moment où j’écris cet article, mais je ne doute pas qu’elle vaille le coup !). Je n’ai pas été déçu du voyage !

On s’échauffe tranquillement avec un raisonnement par l’absurde sur les nombres premiers. On est dans du classique, mais cet exemple est à maîtriser.

L’exercice 2 est de la géométrie. Sans être forcément difficile, il est assez bourrin avec une composition de 4 transformations. Pas mal de calculs, j’espère ne pas avoir fait d’erreur, j’avoue avoir eu la flemme de relire !

On arrive sur le gros morceau, le problème de Bâle ou le calcul de la somme des inverses des carrés. On va donc manipuler des suites dans un premier temps (ça reste le thème de base) pour s’assurer d’abord de la convergence de la somme. On continue ensuite avec de la trigonométrie, en faisant un détour par les complexes tant qu’à faire. Je pense que cette partie n’est plus vraiment accessible en terminale, les complexes n’étant abordés qu’en maths expertes. On s’étonnera au passage qu’un résultat assez basique (la somme des termes d’une suite géométrique) soit rappelé dans l’énoncé quand on voit les connaissances nécessaires pour traiter le problème.

Avant de conclure, on passe par des études de fonctions et des calculs d’intégrales dont on va chercher les limites… L’arrivée à ce magnifique résultat sera la consécration de tous ces efforts !

En selle, voici le sujet :

bac-c-1981-aix-marseilleTélécharger

Et la correction :

Bac C 1981 – Aix Marseille – corrigéTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Bac S 1996 – Asie – corrigé complet

Pour ce dernier post de l’année, je vous propose un dernier sujet de bac que j’ai trouvé plutôt varié et donc intéressant.

On commence avec un exercice de probabilités assez standard. Il reste d’actualité, car on y revoit les formules principales qu’on trouve dans tous les sujets actuels ! (Enfin, c’est l’impression que ça m’a donné ces dernières années). On tire une boule, puis 3 et on passe par les probabilités totales puis conditionnelles.

Comme souvent autour de cette période, l’exercice spécifique à l’enseignement obligatoire s’intéresse aux complexes (ça fait toujours un peu mal de penser que c’est réservé en maths expert maintenant, quand on pense simplement au voyage intellectuel depuis leur « création » jusqu’à leur importance en physique actuellement !). On y étudie une transformation sous un angle analytique puis géométrique. Cela permet de revoir une bonne partie des propriétés du programme, l’utilisation de l’expression conjuguée, les propriétés d’un quotient de 2 complexes…

Pour l’exercice 2 de spécialité, on étudie une fonction paramétrique, là encore en 2 temps : tout d’abord une étude directe puis une étude via une transformation dans le plan complexe. Pour la première partie, je ne sais pas si ça se pratique encore beaucoup aujourd’hui ! En tout cas, je n’en ai pas vu depuis un moment, à part pour des choses très basiques comme des droites ou des plans dans l’espace. Bref, cela oblige à revenir aux bases de certains concepts, comme la dérivée par exemple, on ne peut pas utiliser les formules classiques sous cette forme. La 2ème partie avec la transformation complexe est assez amusante, car finalement on « devine » plus facilement la forme de la courbe ! (Enfin, il faut d’abord connaître le résultat pour pouvoir le proposer cela dit…)

On finit sur un problème d’analyse. On est sur une fonction très standard, qu’on peut trouver encore aujourd’hui d’ailleurs, à base de logarithme. Pas grand chose à ajouter, on va cependant balayer une bonne partie des concepts du secondaire : étude de fonction, intégrales et utilisation de suites pour approcher une valeur particulière.

Au final, un beau sujet pour finir l’année ! J’en profite pour remercier tous ceux qui ont venus sur ce blog pendant l’année, j’espère que ça aura pu vous être utile ou, au moins, que ça aura piqué votre curiosité !

Sujet :

bac-s-1996-asieTélécharger

Corrigé :

bac-s-1996-asie-1Télécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Bac série S 1996 – Métropole groupe II

Nouveau sujet de bac dans ce post, avec le sujet de métropole groupe 2 (je ne sais pas trop où c’est du coup…) en 1996.

On attaque sur un exercice de probabilités avec 2 sacs de 5 boules. On revoit une bonne partie des questions classiques avec le dénombrement de différentes combinaisons, la description d’une loi de probabilité, des probabilités conditionnelles et un loi binômiale pour terminer !

On continue sur l’exercice d’enseignement obligatoire qui porte sur les complexes (dommage de se dire qu’aujourd’hui ce monde merveilleux est réservé à ceux qui prennent maths expertes !). Comme dans d’autres exercices déjà croisés, on est surtout sur l’interprétation géométrique des affixes et transformations du plan : on mélange donc des calculs et l’interprétation du résultat, c’est toujours intéressant !

L’exercice de spécialité est pour sa part un exercice de géométrie. Et… bah franchement, pas grand-chose à voir ! Rien de bien intéressant, la question 2.b à la limite. Quel dommage et surprise par rapport à l’exercice précédent.

On finit sur du classique, un problème d’analyse avec des exponentiels, des études de fonctions et un peu d’intégrales pour finir. Un peu d’originalité avec le f+f^2, sympa !

Encore un bon sujet, qui doit être accessible pour les terminales actuelles et plus intéressant que les annales des dernières années !

À vous de jouer…

bac-s-1996-metropole-groupe-iiTélécharger
bac-s-1996-metropole-groupe-ii-1Télécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Bac série S 1995 – Pondichéry

On continue aujourd’hui notre exploration des sujets de bac en voyageant cette fois dans l’espace en plus du temps pour nous en 1995, époque qu’on connait déjà bien et en Inde à Pondichéry. Nous voilà donc au bord de l’océan indien pour les prochaines heures. Vous noterez que je n’ai traité que les exercices de spécialité, sans aucune raison à part une forme de flemme. J’avoue…

On attaque donc sur un exercice de complexes et leur représentation géométrique. Comme d’hab, on n’insiste jamais trop sur l’importance des complexes pour les études scientifiques dans le supérieur. Rien de particulier, à part une question où je suis parti sur une méthode calculatoire proche de l’enfer. Il est peut-être possible de faire autrement, n’hésitez pas à me dire si vous avez d’autres idées !

J’ai donc zappé l’exercice de probabilités. Mais j’encourage tout de même à le faire.

On continue donc sur l’exercice de géométrie avec des triangles et des transformations. Les concepts revus ici sont donc plutôt simples, mais ils sont à bien maîtriser, c’est là où l’exercice est intéressant.

On finit sur un problème d’analyse. Si vous avez déjà suivi les sujets précédents, on retrouve un peu toujours les même sujets, de l’exponentiel, de la dérivation, de l’intégration, des valeurs approchées de racines. Bref, à force tout le monde doit être très à l’aise !

Lançons-nous !

bac-s-1995-pondicheryTélécharger
bac-s-1995-pondichery-1Télécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine