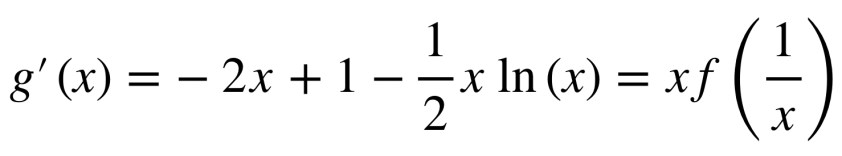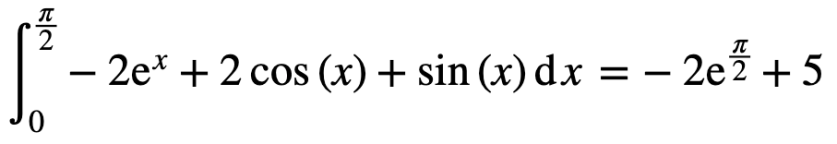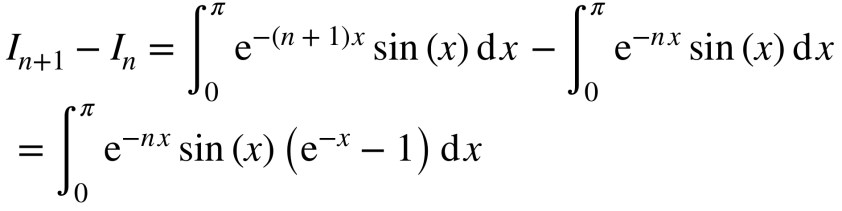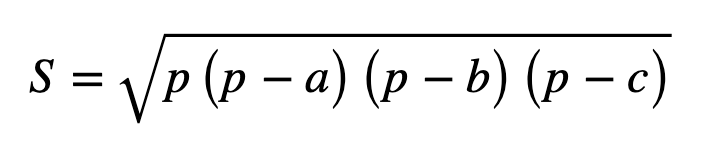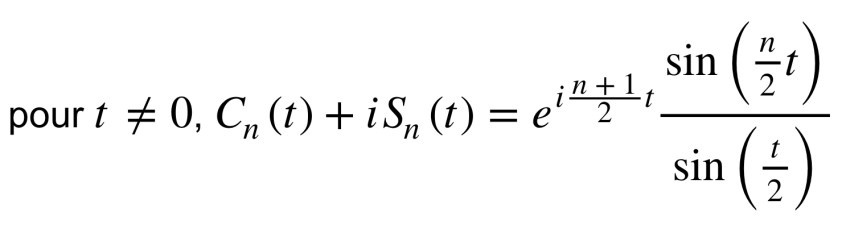géométrie

Bac 2024 – Métropole 1 – corrigé

Je vous propose aujourd’hui le corrigé de l’épreuve « jour 1 » de l’épreuve de spécialité maths en métropole. Cette année encore ça aura fait beaucoup parler, mais assez différemment de l’an dernier, certains l’ayant trouvés trop dure. Alors qu’en est-il ? Voyons ça tout de suite.

On attaque avec un VRAI/FAUX, d’échauffement : 2 questions sur une fonction exponentielle et 2 questions sur des suites. Des questions de cours non triviales, à maîtriser pour marquer les points.

On enchaine sur un des gros morceaux du sujet : les probabilités. On commence sur du très classique : arbre de probabilités, probabilités conditionnelles et loi binomiale, comme dans tous les autres sujets ! La dernière question fait partie de celles qui ont fait parler : l’inégalité de Bienaymé-Tchebichev. Pour le coup, pas vraiment attendu, mais un très beau résultat de probabilité, ça fait plaisir de la croiser ! Enfin, pour les élèves moins j’imagine, elle n’est pas forcément évidente à manipuler et pas sûr que les profs aient le temps d’insister dessus.

Géométrie dans l’espace pour l’exercice 3, là encore assez attendu car proche de ce qu’on a croisé dans les autres sujets. Pas grand chose à dire, à part là aussi la dernière question pour laquelle il faut avoir la bonne idée, sinon c’est bien plus compliqué !

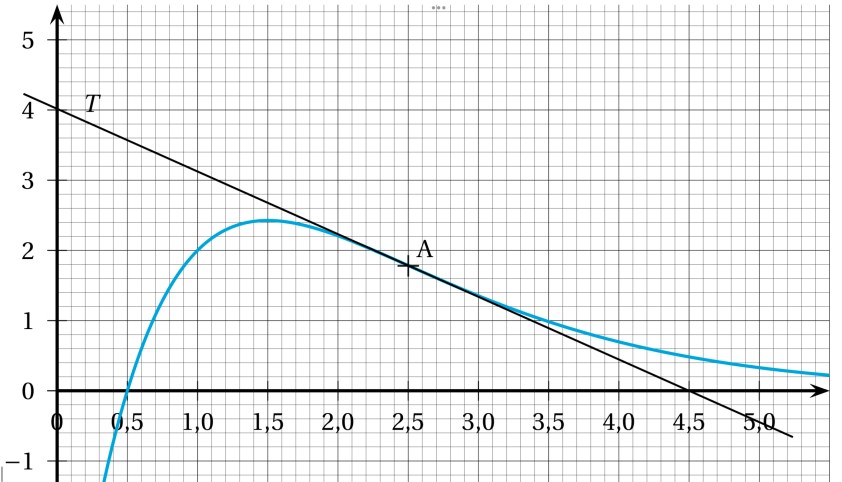
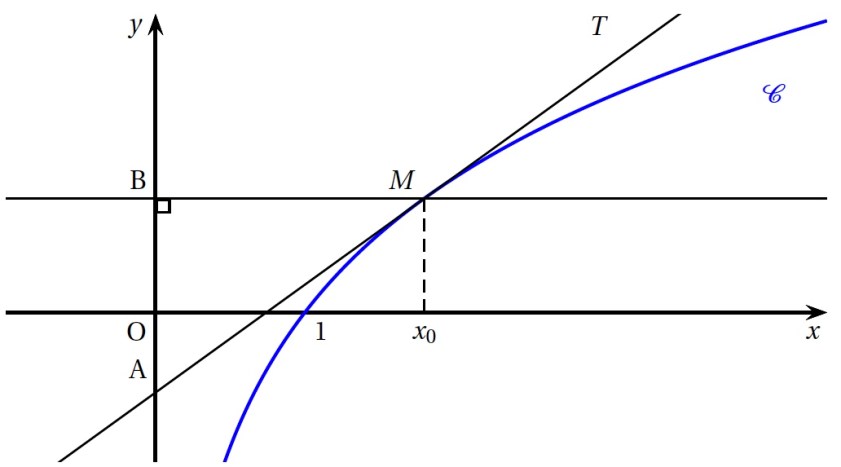
On finit par un exercice d’analyse avec une étude de fonction dont le but est d’arriver sur un calcul d’intégrale. C’est surtout cet exercice qui a pas mal fait causer, mais je ne comprends complètement, la majorité de l’exercice est là encore très classique, même s’il faut manipuler du f\left( \frac{1}{x} \right) . Idem pour l’intégrale à calculer, c’est une intégration par partie, rien d’impossible. Je ne tiens pas non plus à passer pour un vieux con depuis mon canapé et pour préciser ma pensée, le sujet était passablement plus dur que ces dernières années et les réactions me semblent surtout mettre en avant que les élèves s’attendaient à une épreuve bidon. Désolé pour eux ! Je ne connais pas le barème, mais la majorité des questions restent dans le cadre du cours et de ce qu’on peut trouver dans les exercices classiques des annales. Une bonne source de révisions pour les prochains !

Le sujet :

Bac 2024 – Métropole 1Télécharger

Le corrigé :

Bac 2024 – Métropole 1 – corrigéTélécharger

N’hésitez pas à me contacter pour toutes questions et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Bac 2024 – Asie 1 – corrigé complet

Un article rapide pour ce qui sera certainement ma dernière contribution pré-session 2024, je manque un peu de temps en ce moment malheureusement !

Je vais faire le tour rapidement :

Lecture graphique puis analyse sommaire d’une fonction.

Géométrie dans l’espace : je pense qu’on peut mettre une pièce dessus.

Probabilités avec arbre de décision et loi binomiale : une 2ème pièce ?

Quelques affirmations en VRAI/FAUX pour finir !

À votre tour et bon courage à ceux qui révisent !

bac-2024-asie-1Télécharger

Le corrigé :

bac-2024-asie-1-corrigeTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Bac 2024 – Centres étrangers 1 – corrigé complet

On continue à s’entraîner (enfin, pour ceux qui ne sont pas passés, c’est vrai que j’ai tendance à réfléchir en bon métropolitain ) avec cette fois l’épreuve proposé dans les centres étrangers (j’avoue aussi que je ne sais pas exactement quelles géographies se trouvent regroupées dans cette appellation… mais bref !) il y a 2 jours. On se lance sans attendre, on va recroiser des thèmes déjà vus ces derniers temps !

Premier exercice de probabilité, mais cette fois mélangé avec un peu d’analyse avec une fonction qui va nous permettre d’apprécier la précision d’un modèle de contrôle anti-dopage. Merci aux JO pour cet exercice un peu original sur ce thème ! On reste sinon sur un arbre de décision et des probabilités conditionnelles.

On enchaîne sur de l’analyse avec une fonction classique, qui nous amène sur une suite et une boucle Python (qui porte d’ailleurs le même nom que les 2 sujets précédents) à compléter. Je n’ai rien à ajouter, du standard à bien maîtriser !

Un peu d’originalité avec un équation différentielle ! Ca fait plaisir (je ne sais pas si c’est pareil pour les élèves ?). L’exercice en lui-même est classique, on résout une équation différentielle en plusieurs étapes. Un calcul d’intégrale se glisse à la fin, sans transition (enfin, c’est une des fonctions qui intervient dans l’exercice) !

On finit avec de la géométrie dans l’espace avec peu ou prou les mêmes questions que dans le sujet précédent, ça ne tombait plus trop à une époque, je pense que ça vaut la peine de s’y pencher pour ceux qui n’ont pas encore passé l’épreuve. C’est souvent en fin d’année en plus et vu rapidement…

Entre le moment où j’ai commencé et maintenant un autre sujet « centres étrangers » est sorti, je ne l’ai pas encore regardé, on va voir si les tendances se confirment !

Le sujet :

bac-2024-centres-etrangers-1Télécharger

Le corrigé :

bac-2024-centres-etrangers-1-corrigeTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Bac 2024 – Amérique du Nord 2 – corrigé

On continue à réviser. Alors, je ne suis pas familier avec toutes les sessions du Bac et je découvre qu’il y a un 2ème sujet en Amérique du Nord. Le voici donc ! Et toujours merci à l’APMEP, qui partage les sujets très rapidement.

On repart donc, la structure est la même avec 4 exercices de tailles assez comparables et les mêmes thèmes. Du coup c’est un peu moins fun et on n’a pas d’exercice qui nous sort de notre torpeur comme le dernier du précédent sujet.

Allons-y ! On attaque comme la dernière fois avec des probabilités. C’est proche, un arbre pondéré puis un loi binomiale. Les calculs sont juste plus compliqués. Mais qui sont fait avec une calculatrice…

On continue avec la géométrie dans l’espace. Pas original, mais à savoir faire si vous êtes en train de réviser.

On bascule dans l’analyse pour les 2 derniers exercice. Enfin, suite définie par une fonction, donc étude de la fonction et points fixes pour étudier la suite. Encore du classique.

On finit sur une étude de fonction qui est plus proche de la restitution de connaissances puisque la fonction est a\ln \left(x\right). Si vous avez des doutes en le faisant, reprenez le cours !

Je vous conseille de le parcourir si vous êtes en train de réviser !

Le sujet :

bac-2024-amerique-du-nord-2Télécharger

Le corrigé :

bac-2024-amerique-du-nord-2-corrige-Télécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Bac 2024 – Amérique du Nord – corrigé

Je ne sais pas s’il faut dire qu’on continue les révisions ou qu’on attaque les sujets de cette année, mais je vous propose le sujet proposé hier en Amérique du Nord. J’ai vu pas mal de commentaires en particulier sur le dernier exercice et j’ai donc voulu rapidement y jeter un œil. Lançons-nous donc sans attendre ! PS de l’intro : merci à l’APMEP d’avoir partagé le sujet aussi rapidement.

On attaque sur des probabilités, du classique avec un arbre de décision et une loi binômiale. Un classique qui sort souvent sous une forme ou une autre !

Un QCM pour continuer, mais au moins les questions sont reliées entre elles. Il y aurait probablement eu moyen d’en faire un exercice un peu plus cohérent, mais bon, c’est déjà ça. Des droites dans l’espace et des représentations paramétriques. Pas si fréquent, donc un bon entraînement.

Exercice 3 sur une étude de fonction logarithmique. Du classique là encore, donc toujours dans les clous pour les métropolitains qui révisent !

Et on arrive donc sur le dernier exercice qui nous fait étudier une suite définie par des intégrales. On pense aux intégrales de Wallis qu’on a déjà croisé ici (2 fois oui, mais là c’est quand même pas exactement pareil). Celui-ci mélange les fonctions trigonométriques avec des exponentielles. On y manipule les propriétés basiques de ces fonctions et des intégrations par parties. Un exercice bien ficelé et intéressant assez différent de ce qu’on a croisé ces dernières années, ça fait plaisir ! À vous de jouer !

Le sujet :

Bac 2024 – Amérique du Nord 1Télécharger

Le corrigé :

bac-2024-amerique-du-nord-1-corrigeTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

BAC S 2018 – Métropole – corrigé complet

Les révisions du bac vont bon train, je vous propose donc aujourd’hui d’étudier le sujet de 2018 en métropole (et la Réunion d’ailleurs). Je l’ai fait après être tombé sur un bel article du site Images des Mathématiques (hautement recommendable soit dit en passant) : https://images.math.cnrs.fr/Nombres-puissants-au-bac-S.html. Mauvaise pioche, l’exercice évoqué est le dernier du sujet !

On attaque sur un exercice d’analyse dans lequel on étudie une fonction exponentielle. On va chercher des points possédant une propriété particulière en introduisant une autre fonction qu’on va étudier en détails. On glisse un peu d’algorithmique pour finalement arriver sur un cas pratique.

On enchaîne sur un exercice de probabilités évoquant la diffusion d’une maladie, en fonction de la vaccination ou non des individus. Vu l’année, c’était la grippe évidemment ! Pas grand chose à dire, les questions sont très classiques, à maîtriser bien sûr !

L’exercice 3 propose de la géométrie dans l’espace et des propriétés des tétraèdres. On revoit une bonne partie des notions du programme, c’est intéressant. Toujours dommage qu’on n’en voit pas plus.

On bifurque ensuite pour l’exercice hors spécialité, qui nous propose une suite de nombres complexes dont on va étudier le comportement, puis des propriétés des points du plan dont les affixes sont les éléments de la suite. Evidemment, le public cible est plus restreint aujourd’hui, mais ça reste intéressant pour ceux qui sont en maths experts.

Et on finit donc par l’exercice sur les nombres puissants évoqué en introduction ! Exercice d’arithmétique avec un peu de matrice au milieu. Là encore on est sur le programme math expert mais c’est un exercice bien foutu et un bon enchaînement. Enfin, je ne pourrais pas en dire plus que l’article partagé !

Au final, un sujet très intéressant, même s’il ne s’adresse qu’à une frange réduite des élèves aujourd’hui… Enfin, je recommande tout de même pour ceux qui font maths experts ! Allons-y !

Sujet :

bac-s-2018-metropoleTélécharger

Corrigé :

bac-s-2018-metropole-corrigeTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Brevet 2023 – Maroc – corrigé complet

Après avoir longuement parlé du bac marocain, attaquons cette fois le brevet ! Merci comme souvent à l’APMEP pour avoir mis ce sujet à disposition.

On attaque sur un exercice comprenant équation, inéquation et système d’équations. Des questions assez standards pour manipuler ces objets.

Un peu de statistiques pour continuer. Exercice, assez basique sur un tableau de statistiques. Pas de probabilité là, ainsi que dans le reste du sujet. Ça peut étonner, c’est un passage obligatoire chez nous (du moins dans tous les sujets que j’ai regardés).

On enchaîne sur des fonctions linéaires et affines. Un exercice qu’on pourrait tout à fait voir chez nous. De la lecture graphique et du calcul.

L’exercice 4 est un exercice de géométrie, à base de translation. Là encore, toutes les notions sont abordées, mais on calcule plutôt des aires de rectangles ces dernières années !

La suite est actuellement hors programme puisque c’est un exercice sur les vecteurs et les équations de droites. C’est typiquement des exercices qu’on croise en 2nde.

On finit sur de la géométrie dans l’espace avec une pyramide à base carrée. On croise les classiques, Thalès, Pythagore ou des calculs de volume. Là encore, on est dans les clous du programme français, mais je ne sais pas si tout est abordé, car la géométrie dans l’espace arrive souvent en fin d’année et souffre donc souvent du manque de temps pour boucler le programme. Dommage !

Je ne savais pas trop à quoi m’attendre… On constate qu’une partie du sujet correspond au programme de 2nde actuel chez nous. Cependant, la majorité des questions devraient être accessible pour un élève de 3ème. La grosse différence évidemment est le niveau du sujet qui est plus difficile que les sujets récents en France (La formule de volume d’un parallélépipède est rappelée…) ! Et évidemment, on ne retrouve jamais l’horrible mention « aucune justification n’est demandée ». On peut donc tout de même en faire un bon entraînement de fin de 3ème !

Le sujet :

brevet-maroc-2023Télécharger

Le corrigé :

brevet-maroc-2023-corrigeTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

CAPES Mathématiques 2024 – Épreuve 1

Je pense que c’est assez connu, le CAPES est le concours de recrutement des enseignants du second degré, collège et lycée. L’écrit de ce concours est composé de 2 épreuves, une constituée de problèmes dans la discipline concernée et une dans laquelle on évalue des réponses potentielles d’élèves, évidemment toujours dans la discipline. Bref ! Aujourd’hui je vous propose de balayer la première épreuve.

J’ai déjà dit que je n’aimais pas les VRAI/FAUX, où on enchaîne les questions sans rapport les unes avec les autres et où (parfois) tout le sel réside dans une formulation subtilement trompeuse… Bon, après il ne faut pas non plus se chercher des excuses, mais ça ne permet pas des problèmes passionnants. Eh bien me voilà servi avec 23 questions et à peu près la moitié du sujet ! On parcourt une large part des thèmes du lycée avec proportionnalité, analyse (surtout sur les intégrales), arithmétique (et un peu de logique), géométrie (dans l’espace), probabilité et algorithmique. Il faut bien connaître le cours (vous me direz que c’est bien le minimum si on veut être professeur !), mais pas grand chose de palpitant. Qui a dit au fond de la salle que je pouvais réviser la loi de Poisson ?? Oui, bon, ça va hein, ça arrive à tout le monde un moment de faiblesse ! D’ailleurs, à choisir la partie probabilité m’a plutôt plu avec des questions un peu différentes des habitudes.

Passons au problème d’analyse qui va nous faire étudier des modèles d’évolution de populations. Étude de fonction, suites, un peu d’équations différentielles et d’algèbre linéaire à la fin. Le principe est plutôt intéressant et on compare le comportement asymptotique de ces différents modèles.

Au final, pas de grosse difficulté dans le sujet mais une bonne occasion de réviser avant le bac ! Ou même en L1, je pense que ça ne fait pas de mal.

Le sujet :

capes-2024-epreuve-1Télécharger

Le corrigé :

CAPES 2024 – Epreuve 1 – corrigéTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Les fondamentaux – 3 beaux exercices pour finir le calcul algébrique !

Retour sur les exercices de 2nde pour finir le chapitre sur le calcul algébrique. Comme on a déjà pu le voir avec des exercices « avancés », on n’utilise pas forcément des techniques ou concepts plus difficiles, mais il faut parfaitement maîtriser le cours pour pouvoir avoir les bonnes idées.

On attaque avec des manipulations d’expressions littérales (évidemment, c’est un peu le thème) et le 1er exercice ressemble à ce qu’on a déjà pu croiser sur la chaîne Hedacademy pour ceux qui la suive (et que je recommande à ceux qui ne le font pas déjà !) : https://youtube.com/@hedacademy?si=wTQckaJLOe-oZUDg. Je ne dirais jamais assez qui faut connaître par cœur ses identités remarquable et dans les 2 sens !

J’ai un peu menti dans l’introduction, le 2ème exercice demande de connaître une identité remarquable du 3ème degré (ou au moins de savoir que ça existe), sinon on peut chercher un moment ! Le principe est sinon le même que dans l’exercice précédent.

Pour le 3ème, on va faire un peu de géométrie pour démontrer la formule de Héron qui fait le lien entre l’aire d’un triangle et son périmètre (ou plus exactement son demi-périmètre). Je trouve personnellement que c’est une très belle formule, malheureusement pas assez connue. Pour arriver à ce résultat, on par du classique et scolaire « base fois hauteur divisé par 2 » et formuler cela en fonction des longueurs des côtés. Ne cherchez pas à vous esquiver, on va encore passer par des identités remarquable, le calcul d’aires faisant naturellement apparaître des sommes et différences de carrés.

Embarquons pour ce voyage !

livret-2nde-exos-20-a-22Télécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine

Bac C 1981 – Aix Marseille – corrigé complet

Repartons à la rencontre des sujets qui ont fait pleurer les élèves en leur temps avec ce sujet de 81 pour l’académie d’Aix Marseille. J’avais entendu parler de ce sujet il y a quelques temps et il m’est revenu en tête à la publication de la vidéo d’Axel Arno (https://youtu.be/XYKocUhk4Ng?si=cN9XNH4Un6opnOns. Je n’ai pas encore regardé la vidéo au moment où j’écris cet article, mais je ne doute pas qu’elle vaille le coup !). Je n’ai pas été déçu du voyage !

On s’échauffe tranquillement avec un raisonnement par l’absurde sur les nombres premiers. On est dans du classique, mais cet exemple est à maîtriser.

L’exercice 2 est de la géométrie. Sans être forcément difficile, il est assez bourrin avec une composition de 4 transformations. Pas mal de calculs, j’espère ne pas avoir fait d’erreur, j’avoue avoir eu la flemme de relire !

On arrive sur le gros morceau, le problème de Bâle ou le calcul de la somme des inverses des carrés. On va donc manipuler des suites dans un premier temps (ça reste le thème de base) pour s’assurer d’abord de la convergence de la somme. On continue ensuite avec de la trigonométrie, en faisant un détour par les complexes tant qu’à faire. Je pense que cette partie n’est plus vraiment accessible en terminale, les complexes n’étant abordés qu’en maths expertes. On s’étonnera au passage qu’un résultat assez basique (la somme des termes d’une suite géométrique) soit rappelé dans l’énoncé quand on voit les connaissances nécessaires pour traiter le problème.

Avant de conclure, on passe par des études de fonctions et des calculs d’intégrales dont on va chercher les limites… L’arrivée à ce magnifique résultat sera la consécration de tous ces efforts !

En selle, voici le sujet :

bac-c-1981-aix-marseilleTélécharger

Et la correction :

Bac C 1981 – Aix Marseille – corrigéTélécharger

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine