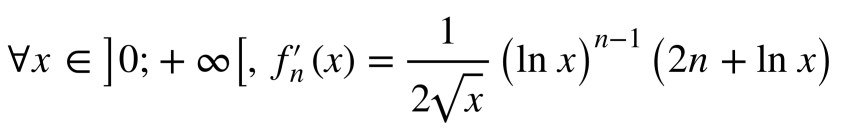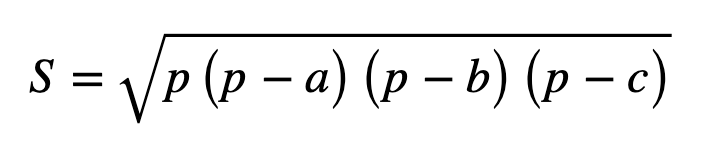Les sujets des épreuves de maths du bac au Maroc sont l’objet de pas mal de discussions tous les ans. Je n’avais pas vu passer jusqu’ici d’épreuve de rattrapage… Je me suis donc penché dessus et le moins qu’on puisse dire est que je n’ai pas été déçu ! Tuons le suspens, je pense qu’il valait mieux réussir la première épreuve, ce rattrapage étant au moins aussi difficile, voir même plus.

Regardons un peu tout ça ! On reste dans l’esprit des sujets que j’ai partagé précédemment et on attaque sur un long exercice d’analyse, découpé en 3 parties : on étudie d’abord les propriétés générales d’une famille de fonctions définies avec un paramètre n. On continue avec une suite définie par une valeur particulière de chaque fonction . Questions classiques de monotonies et limites… On finit par du calcul d’intégrale. Une étude très complète donc et vraiment pas facile !

Les 3 exercices suivants sont plus courts. On enchaîne avec un exercice sur les complexes qu’on introduit via un système de 2 équations à 2 inconnues qui vont être liées aux parties réelles et imaginaires d’un complexe . La 2ème partie n’est pas liée et propose une approche via les complexes d’un problème de géométrie. Dans cette partie, on peut insister une fois de plus sur la puissance des nombres complexes comme « extension » de la géométrie cartésienne.

La suite est « traditionnellement » sur les structures algébriques, mais cette fois, on ne reste pas sur les habituelles (et encore, seulement en maths expertes chez nous) manipulations de matrices, mais on introduit des structures et des opérations assez inédites. Même si ces dernières restent à base d’arithmétique, leur manipulation demande une bonne maîtrise des concepts sous-jacents car on peut vite se perdre sinon !

Pour les survivants, on finit avec un peu d’arithmétique et de congruence. Là encore un exercice assez court, mais pas facile pour autant. On se rappelle si besoin, que sous leur air gentillet, ces exercices peuvent vite demander de se creuser la tête pour trouver les bonnes idées !

En conclusion, encore un très bon cru venu du Maroc, même si je ne sais pas si beaucoup ont eu l’occasion de se rattraper avec cette épreuve ! J’avais récupéré ce sujet il y a un moment, donc je ne sais plus trop où, mais merci à celle ou celui qui avait partagé ! Allons-y !

N’hésitez pas à me contacter pour toute question et à bientôt pour de nouvelles aventures mathématiques !

Antoine